Secara sederhana, relasi dapat diartikan sebagai hubungan. Hubungan yang dimaksud di sini adalah hubungan antara daerah asal (domain) dan daerah kawan (kodomain). Kedua jenis daerah akan dijelaskan kemudian. Sedangkan fungsi adalah relasi yang memasangkan setiap anggota himpunan daerah asal tepat satu ke himpunan daerah kawannya. Perbedaan antara relasi dan fungsi terletak pada cara memasangkan anggota himpunan ke daerah asalnya.
Pada relasi, tidak ada aturan khusus untuk memasangkan setiap anggota himpunan daerah asal ke daerah kawan. Aturan hanya terikat atas pernyataan relasi tersebut. Setiap anggota himpunan daerah asal boleh mempunyai pasangan lebih dari satu atau boleh juga tidak memiliki pasangan. Sedangkan pada fungsi, setiap anggota himpunan daerah asal dipasangkan dengan aturan khusus. Aturan tersebut mengharuskan setiap anggota himpunan daerah asal mempunyai pasangan dan hanya tepat satu dipasangkan dengan daerah kawannya.
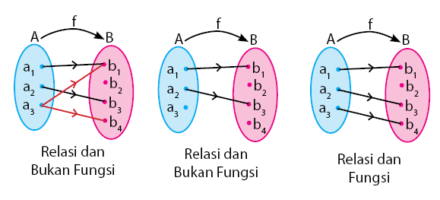
Kesimpulannya, setiap relasi belum tentu fungsi, namun setiap fungsi pasti merupakan relasi. Penjelasan mengenai relasi dan fungsi dapat dilihat pada gambar di bawah.
Selanjutnya, mari simak pembahasan lebih lanjut mengenai relasi dan fungsi pada pembahasan di bawah.
Daerah Asal, Kawan, dan Hasil
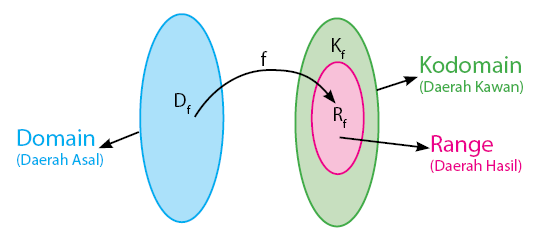
Dalam pembahasan relasi dan fungsi, himpunan yang terlibat digolongkan ke dalam tiga jenis daerah. Ketiga daerah tersebut adalah daerah asal (domain), daerah kawan (kodomain), dan daerah hasil (range). Secara umum, himpunan ketiga daerah tersebut dapat dilihat pada gambar di bawah.
Baca Juga: Sifat-sifat dan Contoh Soal Komposisi Fungsi
Relasi
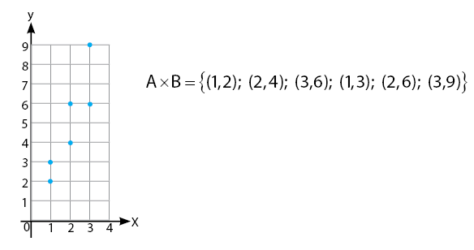
Seperti yang telah dijelaskan secara singkat di atas, relasi dapat diartikan sebagai hubungan. Misalkan sebuah relasi menyatakan hubungan perkalian. Hasil relasi tersebut dapat dinyatakan dalam himpunan pasangan terurut x dan y dan dapat juga digambar pada bidang kartesius.
Cara menyatakan hasil relasi perkalian antara himpunan A dan B dapat dilihat pada contoh permasalahan di bawah.
Pembahasan selanjutnya adalah mengenai fungsi, simak dengan baik sammpai akhir ya!
Fungsi atau Pemetaan
Fungsi atau yang sering disebut juga dengan pemetaan masih termasuk dalam relasi. Suatu relasi disebut fungsi jika semua anggota himpunan daerah asal dipasangkan tepat satu ke daerah kawannya.
Simbol fungsi yang memetakan himpunan A ke B adalah
Contoh pemasalahan pada fungsi:
Diketahui himpunan A dan B diberikan seperti di bawah.
Didefinisikan fungsi  dengan f(x) = x + 5.
dengan f(x) = x + 5.
Tentukan hasil pemetaan dari  oleh fungsi
oleh fungsi  ,
,  ,
,  , dan
, dan  !
!
Pembahasan:
Peta dari  oleh fungsi f yaitu y = f(x):
oleh fungsi f yaitu y = f(x):
Daerah Hasil =
Sifat-sifat Fungsi
Fungsi dikelompokkan menjadi 3 (tiga) jenis yaitu fungsi Injektif, Surjektif, dan Bijektif. Pengelompokkan tersebut didasarkan pada sifatnya. Perbedaan ketiga jenis tersebut dapat disimak pada penjelasan di bawah.
- Fungsi Injektif/Fungsi Into (Fungsi Satu-satu)Fungsi pertama yang akan dibahas adalah fungsi injektif atau sering disebut dengan fungsi into atau fungsi satu-satu. Fungsi
dikatakan fungsi injektif jika dan hanya jika anggota kodomain hanya dipasangkan satu kali dengan anggota domain.
Pada fungsi injektif, anggota himpunan daerah kodomain boleh tidak memiliki pasangan, namun semua anggota kodomain yang terpsangkan hanya ada satu, tidak boleh ada yang lebih dari satu.Perhatikan gambar di bawah untuk melihat lebih detail mengenai perbedaannya.
- Fungsi Surjektif (Fungsi Onto)Fungsi Surjekti atau onto memiliki ciri yaitu anggota kodomainnya boleh memiliki pasangan lebih dari satu, namun tidak boleh ada anggota kodomain yang tidak dipasangkan. Fungsi surjektif biasanya dipenuhi apabila jumlah anggota kodomain sama atau lebih banyak dari anggota domain.Perhatikan gambar di bawah untuk menambah pemahan sobat idschool tentang sifat fungsi surjektif.
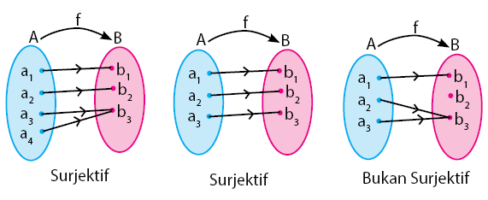
- Fungsi Bijektif (Korespondensi Satu-satu)Fungsi Bijektif merupakan gabungan dari fungsi injektif dan surjektif. Pada fungsi bijektif, semua anggota domain dan kodomain terpasangkan tepat satu. Kebalikan fungsi dari fungsi injektif dan surjektif belum pasti fungsi/pemetaan, namun kebalikan fungsi dari fungsi bijektif juga merupakan fungsi/pemetaan. Perhatikan gambar di bawah.







0comentários:
Post a Comment